「森」姓の人はプロ野球選手になる確率が高い気がする問題

2021年5月17日2021年5月30日

このウェブサイトで誰も頼んじゃいないのに紹介しているプロ野球POGでは、実際のプロ野球選手の成績を使って架空チームの成績を計算しますが、計算用Excelシートは選手名をキーにして選手成績を検索しています。本当は(チーム)＋(背番号)とか、絶対に被らない番号等をキーにした方が良いのでしょうが、日本人の名前は同姓同名が少ないので大きな問題なくできています。外国人だと「マルティネス」が何人もいたりして無理だったでしょうね。

そんなこんなでゲームをしていると選手名に触れる機会が多く、そんな中でふと思ったことがあります。「森」姓の野球選手って、(普段の生活で「森」さんに出会う確率よりも)多い気がする。しかも有力選手が多い、強打の捕手、森友哉に、ホークスの守護神、森唯斗、ベイスターズのドラ1遊撃手森敬斗もいます。ひょっとして「森」姓は野球選手になりやすい？あの名監督森祇晶も兄弟でプロ野球選手だったし・・・。という訳で「『森』姓の人はプロ野球選手になる確率が高い気がする問題」について考えてみました。

「『森』姓はプロ野球選手になりやすい」と言えるのか？

実際支配下選手に「森」姓は何人いるのか？森唯斗(H)、森友哉(L)、森敬斗(DB)、森博人(D)の4人でした。あれ？こんなもん？森唯斗と森友哉が目立っているので印象が強かっただけ？・・・まあとにかく全国苗字ランキングで「森」姓の人の数を調べ、日本総人口(≒1億2600万人と想定)中の「森さん」のパーセンテージと、プロ野球選手(12球団の支配下選手(日本人)の合計＝730人(2021.5.15調べ))の中の「森選手」のパーセンテージを比較してみます。

	全国		支配下選手(日本人)
	人数	比率	人数	比率
森	約463,000	0.367%	4	0.548%
佐藤	約1,862,000	1.474%	7	0.959%
鈴木	約1,791,000	1.418%	11	1.507%
田中	約1,330,000	1.053%	10	1.370%
全体	(てきとう)126,300,000	100%	730	100%

ついでによくある苗字の佐藤、鈴木、田中についても調べました(高橋は髙橋(異字体)もあってややこしいのでやってない)。いちおう、「森」は全国的には0.367%なのに、プロ野球選手に限れば0.548%、比率的には1.5倍くらいになっています。

おお、やっぱり「森」はプロ野球選手になりやすいんじゃん、いやいや、単なる偶然でしょ・・・どっちやねん！？こういう問題に白黒つけようやないか、というのが統計の「検定」というやつです。今回の場合だと、

• 「森」姓も他の姓もプロ野球選手になる確率は変わらない（プロ野球選手が「森」姓である確率は全人口に対する森姓の割合である0.367%と等しい）

という仮説を立てて、この仮説が「間違っている」ことが言えれば「どうやら『森』姓はプロ野球選手になりやすいみたいだぞ」ということになります。実際に確認してみます。

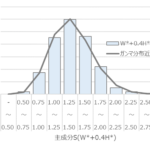
「森」姓である確率が0.367％だとすると、平均で約2.7人が森選手となります。当然2人のときもあれば3人のときもあり、物凄く低い確率ですが10人になる可能性もあります。ただ図に示すように95％以上は0人から6人の範囲に収まるので、森選手が7人以上いると「\(p=0.367\%\)の可能性は低いぞ！？」となり仮説「『森』姓も他の姓もプロ野球選手になる確率は変わらない」は否定^※され、「『森』姓と他の姓でプロ野球選手になる確率は違うみたいだ」となります。

※正確には「棄却される」というそうです。今回の場合5％の確率で仮説が正しい可能性もあるので、「危険率5％で棄却」が正しい表現です(が、堅苦しいのでここでは単に「否定」って書いてます)。

今回の場合4人なので仮説は否定されません。その場合「『森』姓も他の姓もプロ野球選手になる確率は変わらない」という結論にはなりません。否定はされないけど積極的に肯定された訳でもないので「『森』姓も他の姓もプロ野球選手になる確率は変わらないかもしれないし、変わるかもしれない」という何の役にも立たない結論しか出てきません。統計の検定って、結構無力なんですよ。

結局「森」姓がプロ野球選手になる確率はどれくらい？

いまわかっていることは

• 観測結果：プロ野球選手730人中4人(0.548％)が「森」姓だった

であり、その事実からは、プロ野球選手が「森」姓である確率\(p\)は、\(p=0.548\%\)が一番尤もらしい、と考えられます。図にかくとこう。

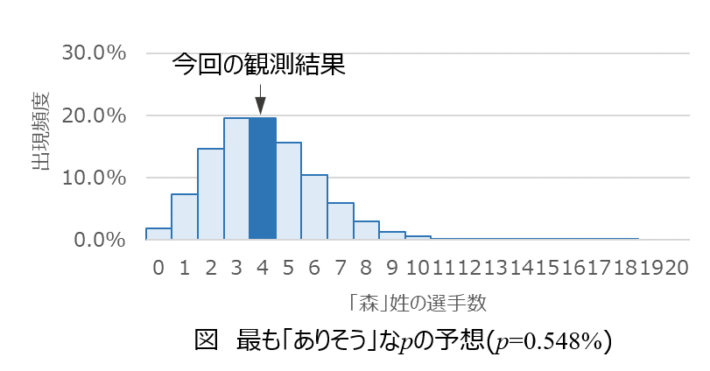
\(p=0.548\%\)のとき、森選手が4人いる確率が最も高くなります。でも、プロ野球選手が「森」姓である確率\(p\)は0.548％よりもっと低いかもしれないし、

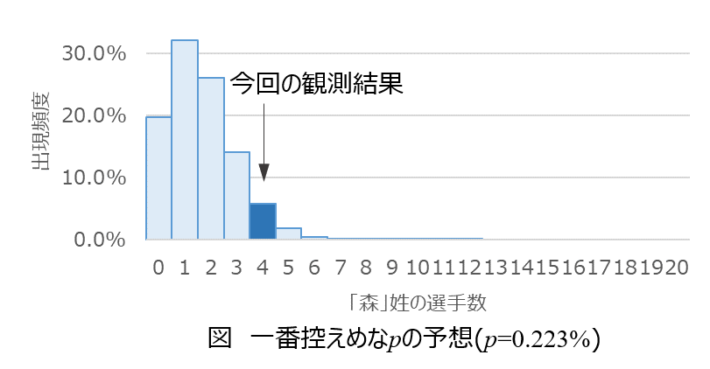
実はもっと高い確率なのかもしれません。

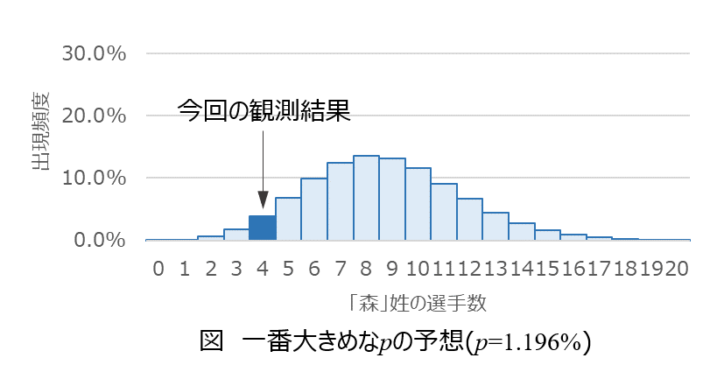
結局「森」姓の選手数が4人であっても納得できる(否定されない)\(p\)の範囲は、

\(0.223\%\leq p \leq 1.196\%\)

となります。全然絞り込めていませんね。先の検定では「『森』姓も他の姓もプロ野球選手になる確率は変わらないかもしれないし、変わるかもしれない」という結論でしたが、これがその理由です。

だいたい、数回しか起こっていないような出来事(今回だとたった4人しか「森」がいない)から、何か結論めいたことを言えというのが無理な話なのです。別の言い方をすると、非常にまれにしか起こらないことを評価しようと思ったら、730回(人)程度の試行ではまだまだ全然足りない、です。もっと試行回数(人数)が必要なのです。今回の例で、支配下選手数が増えた場合の「納得できる\(p\)の範囲」(95％信頼区間)の変化を下の図に示します。

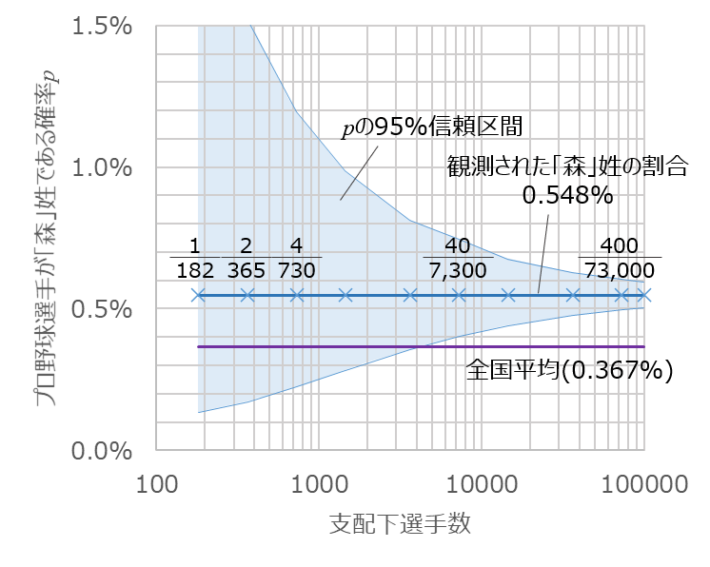
同じ「森」姓の割合0.548％でも、7300人中の40人ならば検定の結果は「『森』姓と他の姓でプロ野球選手になる確率は違うみたいだ」となります。

結論めいたことは言えない、という結論

結局今回の「『森』姓の人はプロ野球選手になる確率が高い気がする問題」は、結論が出ないというのが結論みたいなもんです。でも世の中、今回みたいな話で結論めいたことを言っていること(人)って、結構多いですよね？ナンバーズの法則とか、株の必勝法とか、個人的経験に基づく血液型性格占いとか・・・。

まあナンバーズとか株とか血液型性格占いは、楽しいからわざと言っていることも多いからいいですけど、例えば製品事故なんかで勘違いすると辛いですよね。「Aの建物では50台中1台しか故障しないのに、Bの建物では50台中5台も故障した。AとBの建物の違いに何かヒントあるかもしれない」なんて偉い人が言い出すと厄介きわまりない。空振りに終わる可能性大、といって「単なる偶然です」と証明することもできないし・・・。

という訳で、「結論めいたことは言えない」という結論も、時には大事だと思うんです。