「誰を四番に据えるのか？」といった打順の話は野球のチーム編成では定番かつ人気の話題で、贔屓チームの打順を考えるだけで楽しいものです。打線はドラマに似ていて、役者に役が割り当てられるように打者にも役割があり、シナリオを書くように打順を組み立てます。そのチームの理想の得点パターンを思い描き、幸せな妄想が膨らむところが、打順を考えるときの楽しさでしょう、現実はなかなか妄想通りにはいかないですが。

打線におけるチームプレーとセイバーメトリクス

打席は投手vs.打者の個人プレーですが、打席を打順で並べて打線にすると、チームプレーになります。なぜチームプレーと言えるかというと、それぞれの打者が役割を分担して、チームとして得点を上げるからです。

チーム得点はおおざっぱに言うと①出塁する、②走者を還す、というステップで入るので、打者の役割も、①出塁する、②走者を還す、の二つに分けられます。①はセイバーメトリクスで言う「得点期待値を上げる」ことに相当し、②は「打点を上げる」ことに相当します。セイバーメトリクスの評価の基本となる「得点価値」は、①と②の合計です。

\((得点価値)＝(得点期待値の増減)＋(得点の変化)\)

プロ野球ペーパーオーナーゲームで得失点予測に使っているXRも、打者が生み出した得点価値を表します。各打者のXR＝得点価値を足したものが、チームの得点期待値とほぼ等しくなります。

打率、打点、本塁打といった、昔から注目されてきた打者指標は、どちらかというと②走者を還す役に偏った評価になっていましたが、セイバーメトリクスによって①出塁する役も正しく評価されるようになりました。

セイバーメトリクスによる中田翔評価問題

セイバーメトリクスの得点価値による評価というのは、合理的で良さそうに思えますが、ちょっとした問題もあります。

2018年、ファイターズの四番打者として25本塁打、106打点を記録した中田翔のXRは75.7、タイガースの一番打者に定着し、86個の四球を選んで数多くのチャンスを演出した糸原健斗のXRは77.7でした。XRの値は同程度ですが、中田翔は打点は多いけど得点期待値の増減ではマイナス、糸原健斗は逆に打点は多くないけど得点期待値の増減が大きくプラスと、評価の内訳は大きく違います。

ではこの二人が同じチームにいたとして、二人が稼ぐチームの得点期待値は単純にXRを足し合わせた77.7＋75.7＝153.4となるか？というと、現実の野球ではそう単純にはいきません。打順によってチームの得点力が変わるからです。

(糸原)→(中田)という打順であれば、糸原がチャンスを作り、中田が還すという理想的な得点パターンができあがりますが、(中田)→(糸原)という打順だと、中田翔の打席で走者がいないので打点は稼げない、糸原がチャンスを作っても後ろに還す選手が居ない、となって打線が機能しないでしょう。

XRのような得点期待値での評価は、平均的には正しいでしょう。しかし、個々の選手についてみると、その選手のチームへの貢献度は何番を打つのか、前後の打者が誰なのかによっても変わります。XRの中田翔評価は、言ってみれば一番打者としての中田翔と四番打者としての中田翔の平均です。実際の中田翔はほぼ四番しか打たないので、この平均はすごく無意味です。つまり打順のことまで考えるとXRの評価は常に適切とは言えないのです。

(2020.2.22追記)と、ここまで尤もらしく書いていますが、セイバーメトリクス的には打順の影響は軽微であるというのが定説です(参考文献：セイバーメトリクス入門　　脱常識で野球を科学する)。要はこのページに書いてあることはフィクションです。現実の野球は違うかもしれません。

中田翔の活躍を再現する

プロ野球ペーパーオーナーゲームでは基本的に各打者のXRの合計で架空チームの得点を予測します。しかしこの方法では打順をアレコレ考えて楽しむこともできないし、中田翔が100打点を上げて活躍することも再現できません。これはチーム編成を考えて楽しむゲームとしては致命的です。そこでプロ野球POGに打順の効果を入れ、中田翔のような選手も活躍できるようにすることを考えます。

(2020.2.20追記)繰り返しますが、セイバーメトリクスでは打順の影響は小さいというのが定説です。でも、打順の効果があった方が絶対ゲームとして面白いと思うのです(参考：ドカベン (文庫版) 【コミックセット】明訓高校対弁慶高校…打順が生みだすドラマの最高の例です)。なので敢えて(確信犯的に)打順の効果をゲームに組み込んでいます。

打点創出力XRBI

打順の効果を再現するために、先ず①出塁する＝得点期待値の増減と、②走者を還す＝打点を分けて評価することを考えます。XRは得点期待値の増減と打点の和ですから、得点期待値の増減か打点のどちらかがわかれば、もう片方もわかります。

得点期待値の増減を求めるのは難しいですが、打点は比較的簡単に予測できます。打点が上がるプレーは、主に四死球、単打、二塁打、三塁打、本塁打、犠飛です(細かく言えばスクイズや併殺くずれでの得点などもありますが)。これらのプレーで平均で何点打点が入るのかは、状況別発生確率があればおおよそ予想できます。例えば、本塁打、三塁打、四死球、犠飛の平均打点は次式で出せます。

\((本塁打の平均打点)=\sum_{状況}{(走者数)}\times{(発生確率)}＋1\)

\((三塁打の平均打点)=\sum_{状況}{(走者数)}\times{(発生確率)}\)

\((四死球の平均打点)=(満塁の発生確率)\)

\((犠飛の平均打点)=1\)

単打、二塁打の打点は一意に決まりませんが、これもだいたいは予想できます。これらの予想を使って、打点創出力XRBIを定義します。XRBIは日本野球機構の公式記録に下表の係数を掛けて求めます。係数は各プレーの平均打点に相当します。

表　打点創出力XRBIの係数

安打	二塁打	三塁打	本塁打	盗塁
0.246	0.269	0.393	1.393	ー
盗塁刺	犠打	犠飛	四球	故意四球
ー	ー	1.000	0.026	-0.026
死球	三振	併殺打	打数－安打－三振
0.026	ー	ー	ー

実際のチーム得点とXRBIを比較すると下図のようになります。

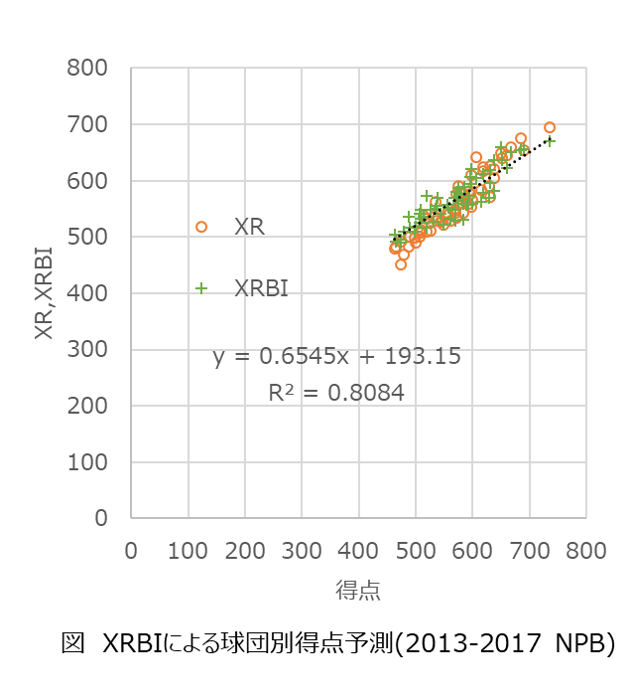
XRほどではないですが、XRBIでもそこそこチーム得点を予測できており、妥当な打点予測となっていると思われます。

XRとXRBIをプロットすると、下図のようになります。XRとXRBIはおおよそ比例関係にあります。

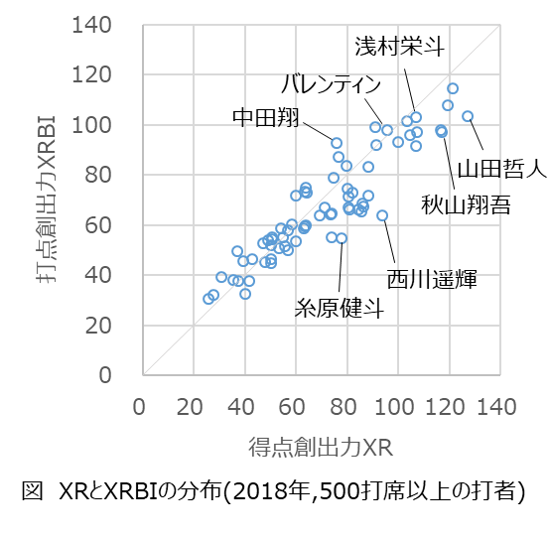
打点創出力XRBIと得点期待値創出力XR-XRBIでプロットすると、下図のようになります。中田翔と糸原健斗はXRでは同程度ですが、打者としてのタイプが全く違うことがよくわかります。

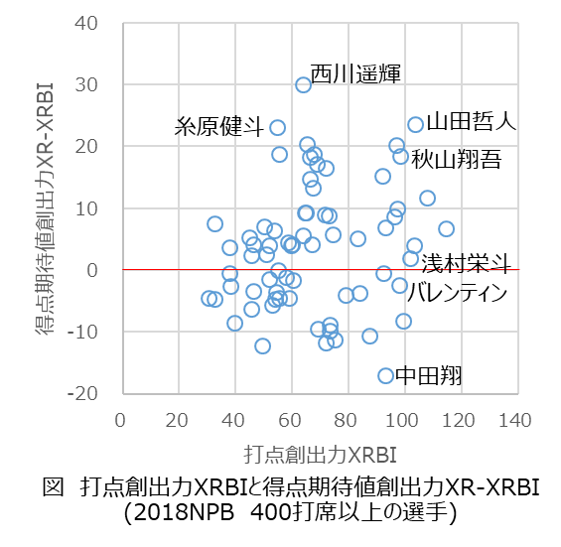
得点期待値倍率REM

得点期待値を増やした打者、即ちXR-XRBIがプラスの打者は、打点が上がりやすい状況をつくり、結果として後の打者の打点を平均でXR-XRBI分増やします。しかし、後の打者の能力次第で、平均以上に打点が増えることも、期待したほど増えないこともあります。プロ野球POGでは、「得点期待値が増えたことによる打点の増加分は後の打者の打点創出力XRBIに比例する」と仮定して、得点期待値倍率\(REM\)(Run Expectancy Magnitude)を新たに定義し、ある打順\(i\)で上げたチーム得点\(R^i\)を次の形で表すことを考えます。

\(R^i=REM_o^i\cdot{XRBI^i}\)

この形にするためには、「打点を平均でXR-XRBI点増やした」を「打点を平均でX倍にした」という形に書き直す必要があります。平均得点を基準として、打者が後に続く打順の打点を何倍にしたかを示す\(REM_b\)を次式で定義します。

\(REM_b=1+\frac{XR-XRBI}{\overline{R}/9}\)

\(\overline{R}=(1試合あたりの平均得点)\times(試合数)\)

※一試合当たりの平均得点は4.01点(2012～2017年NPB平均)です。

\(REM_b\)は打者の能力であり、ある打順における得点期待値倍率\(REM_o\)とは異なります。\(REM_o\)は、1つ前の打者の\(REM_b\)だけでなく、2つ前の打者の\(REM_b\)、3つ前の打者の\(REM_b\)・・・も影響するはずです。また1つ前の打者の\(REM_b\)の影響が最も大きく、打順を遡るに従って影響は小さくなるでしょう。そこで打順\(i\)における得点期待値倍率\(REM^{i}_o\)は、前の打順の得点期待値倍率\(REM^{i-1}_o\)と前の打者の得点期待値倍率\(REM^{i-1}_b\)の幾何平均^※1である、とします。

\(REM^{i}_o=\sqrt{REM^{i-1}_o\cdot{REM^{i-1}_b}}\)

上式を書き下すと、

\(REM^{i}_o={(REM^{i-1}_b)}^{1/2}\cdot{{(REM^{i-2}_b)}^{1/4}}\cdot{{(REM^{i-3}_b)}^{1/8}}\cdot{{(REM^{i-4}_b)}^{1/16}}\cdots\)

となります。 \(REM_o\) は、打順を遡るほど影響が小さくなるように重みを付けた\(REM_b\)の平均値といえます。例えば全打者の \(REM_b\) が同じなら、 \(REM_o\) と \(REM_b\)は等しくなります。

中田翔と糸原健斗で打線を組んでみる

XRBIとREMで本当に打順の効果が再現できるのか、試しに打順を組んで確認します。糸原健斗だけの打線、中田翔だけの打線、糸原健斗と中田翔をミックスした打線を考えます。

表　全員糸原健斗の打線

打順	打者	R	REM_o	XRBI	REM_b	(XR)
1	糸原　健斗	67.3	1.23	54.6	1.36	77.7
2	糸原　健斗	70.7	1.30	54.6	1.36	77.7
3	糸原　健斗	72.5	1.33	54.6	1.36	77.7
4	糸原　健斗	73.4	1.35	54.6	1.36	77.7
5	糸原　健斗	73.9	1.35	54.6	1.36	77.7
6	糸原　健斗	74.1	1.36	54.6	1.36	77.7
7	糸原　健斗	74.2	1.36	54.6	1.36	77.7
8	糸原　健斗	74.3	1.36	54.6	1.36	77.7
9	糸原　健斗	74.3	1.36	54.6	1.36	77.7
	合計得点	654.8				698.9

表　全員中田翔の打線

打順	打者	R	REM_o	XRBI	REM_b	(XR)
1	中田　翔	76.6	0.83	92.8	0.73	75.7
2	中田　翔	72.1	0.78	92.8	0.73	75.7
3	中田　翔	69.9	0.75	92.8	0.73	75.7
4	中田　翔	68.9	0.74	92.8	0.73	75.7
5	中田　翔	68.4	0.74	92.8	0.73	75.7
6	中田　翔	68.1	0.73	92.8	0.73	75.7
7	中田　翔	68.0	0.73	92.8	0.73	75.7
8	中田　翔	67.9	0.73	92.8	0.73	75.7
9	中田　翔	67.9	0.73	92.8	0.73	75.7
	合計得点	627.8				681.1

表　糸原健斗と中田翔をミックスした打線

打順	打者	R	REM_o	XRBI	REM_b	(XR)
1	糸原　健斗	52.8	0.97	54.6	1.36	77.7
2	糸原　健斗	62.6	1.15	54.6	1.36	77.7
3	中田　翔	116.1	1.25	92.8	0.73	75.7
4	糸原　健斗	52.2	0.96	54.6	1.36	77.7
5	糸原　健斗	62.3	1.14	54.6	1.36	77.7
6	中田　翔	115.8	1.25	92.8	0.73	75.7
7	糸原　健斗	52.1	0.96	54.6	1.36	77.7
8	糸原　健斗	62.2	1.14	54.6	1.36	77.7
9	中田　翔	115.7	1.25	92.8	0.73	75.7
	合計得点	691.8				693.0

糸原健斗のみ、中田翔のみの打線よりも、糸原健斗と中田翔をミックスした打線の方が格段に得点力アップしました。これは糸原健斗がチャンスを作って中田翔が還すという良い流れができたおかげです。

XRBIとREMという二つの指標を使った比較的シンプルなモデルですが、色んなタイプの打者が異なる役割を演じ、チームプレーで得点を挙げるという打線の面白さをうまく再現できたと思います(自画自賛)。これでゲームでも打順をアレコレいじってみたり、中田翔のような選手を活躍させたりといったことができるようになりました。