ダンボールクリスマスツリーが素晴らしく平凡であることについて
「それまでの絵が誰かの真似だってわかったんだよ、どこかで見たことあるって。自分の絵を描かなきゃって。」(絵描きの女の子の言葉 映画『魔女の宅急便』より)
このシーンが凄く好きで、それで前回に引き続き引用です。自分の絵を描いたつもりだったのに、出来上がったものは他人の絵だった。私だったら誰かの真似でいいからキレイな絵が描ければそれで満足するでしょう。でも絵描きは満足できません。私の描きたかったものはこれじゃないと絵描きの血が言うのです。
個性的であればいいというものでもない
絵描きと私とでは天と地ほどの差があり、絵描きの姿がまぶしく見えるのは事実ですが、それはそれとして最近(ていうかもう10年以上前から)の誰彼かまわず、無条件かつ闇雲にオリジナリティや個性的なことをありがたがる風潮には少々違和感を感じます。だいたい個性というものの多くは「出そうとして出すもの」じゃなくて「出す気がなくても(出したくなくても)でちゃうもの」であって、あんまりいいものじゃないです。実際、論文や報告書、仕様書、設計図面、ゴルフのスイング、ダイエット法などで個性的なものは大抵ロクでもない結果になります(そして悲しいかな、多くの人が個性的です)。
完成度の高い工作ほど没個性的になる
論文や報告書やらは個性的だとダメな場合が多いと書きましたが、では逆にどういうものがいいかというと、客観的、普遍的、汎用的な内容が、一般的、標準的、定型的な記述で書いてあるものです。没個性の極みですね。絵や小説と違い、論文や報告書(や世の中のいろんなもの)は個性がない方がよい、洗練されるほど個性的ではなくなるものなのです。私にとっての工作もそう。(主に娘の宿題や要望に応えるために)「できるだけ安く、早く、簡単かつ確実にモノを作る方法」を突き詰めると、没個性的な作品になることが多いです。
ダンボールクリスマスツリーがいかに没個性的であるか
このウェブサイトで紹介しているダンボールで作るクリスマスツリーは極めて没個性的な仕上がりです。誰もそんなこと気にしないし頼まれてもいませんが、ここではその一部始終を説明したいと思います。
製作コンセプト1:同じ比率で縮小コピーした段を積み重ねてツリーを作る
なぜこんなコンセプトでダンボールクリスマスツリーを作ろうと思ったかというと、大きいツリーを作りたいけど大きいダンボールが手元に無かったからです。それで分割して作ろうと思った訳ですが、同じ形状のものを縮小コピーして積み重ねてより大きなものを作る、というのは非常によく見かけるパターンですよね。跳び箱、三段重ねのウェディングケーキ、巻貝、ハノイの塔(Wikipedia)などいろいろあります。私が真っ先にイメージしたのは宇宙からきたかんづめ 佐藤さとるファンタジー童話集10 (講談社文庫)にある、塔のお話。誰もてっぺんまで登ったことのない円錐型の塔の秘密は・・・相似形だの級数の収束だの小難しい言葉を使わなくても、この童話を読めばそれがどんなものかイメージできます。
宇宙からきたかんづめ製作コンセプト2:積み重ねるひとつひとつの段は3つのパーツを三角形に組んで作る
別に四角形でも五角形でも良いですが、一番パーツの数が少なく済むのは三角形なので三角形にします。至極当然の選択と言えるでしょう。
パーツの図面
ダンボールクリスマスツリーのパーツ形状は基本的に1種類しかありません。同じ形のパーツ3つを組んで一つの段ができます。更にパーツを縮小コピーすると上の段のパーツになります。このパーツは下図のような手順で作図できます。
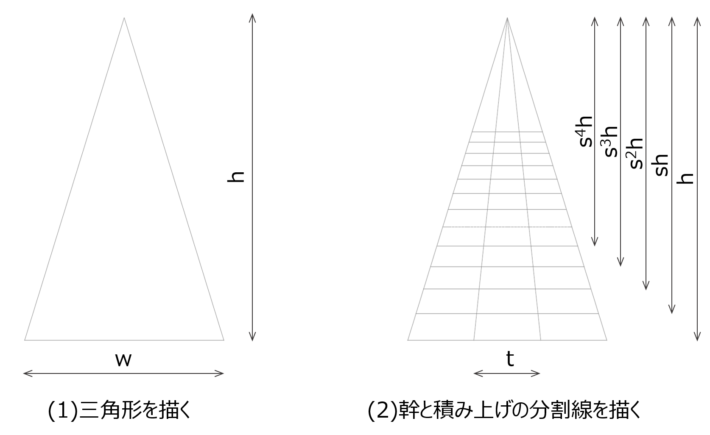
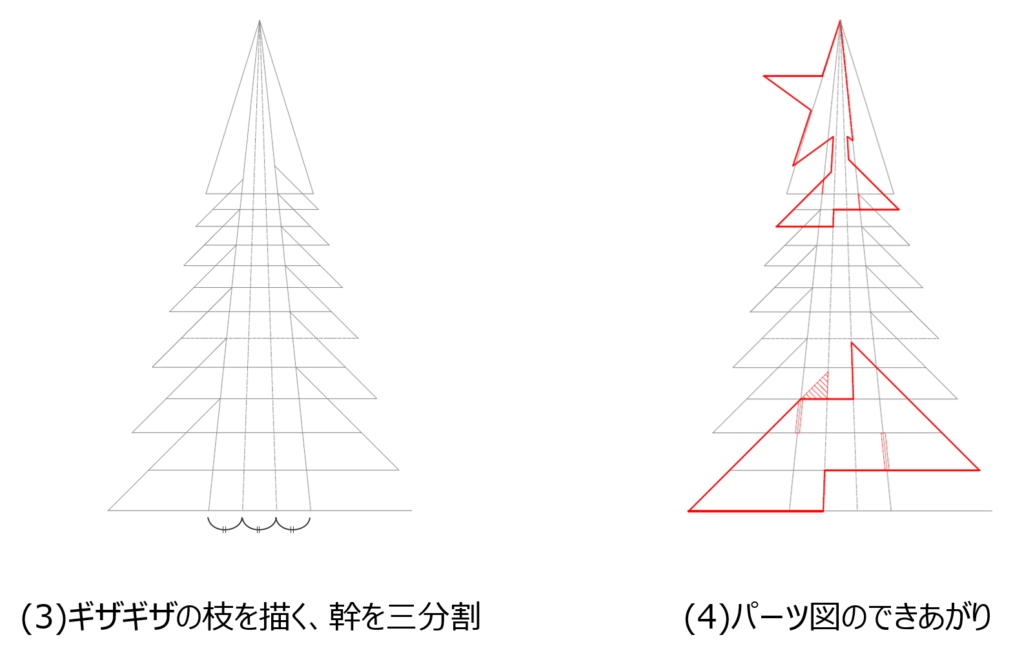
見てのとおり、とても簡単に作図できます(なお(4)のハッチング部分は「あってもいいけど切るのが面倒だからなくした部分」です)。更にツリーの高さhや幅w、幹の幅t、縮小率sを変えて作図すれば、横に広がったツリー、幹が太いツリー、段数が細かく分割されたツリーなど、いろんなタイプのクリスマスツリーを作ることもできます。一番上の段だけはちょっと変形パターンで星を付けていますが、それはデザイン上の理由というより 宇宙からきたかんづめ の塔のお話で、てっぺんまで登った人がいないのと同じ理由からです。
wとhの比は黄金比
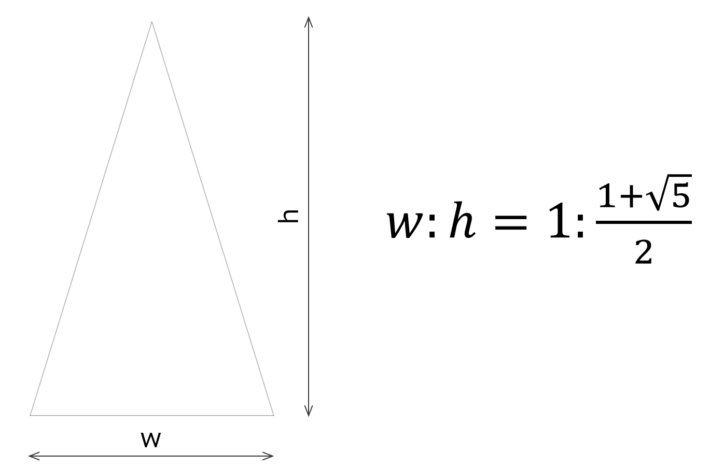
ツリーの高さhと幅wはやっぱり黄金比\(w:h=1:\frac{1+\sqrt{5}}{2}\)にするべきでしょう。別に黄金比である必然性はないけど、「縦横比は黄金比なんだよ」というとなんだかわからないけど物凄く説得力があります。
縮小率sは白銀比から決める
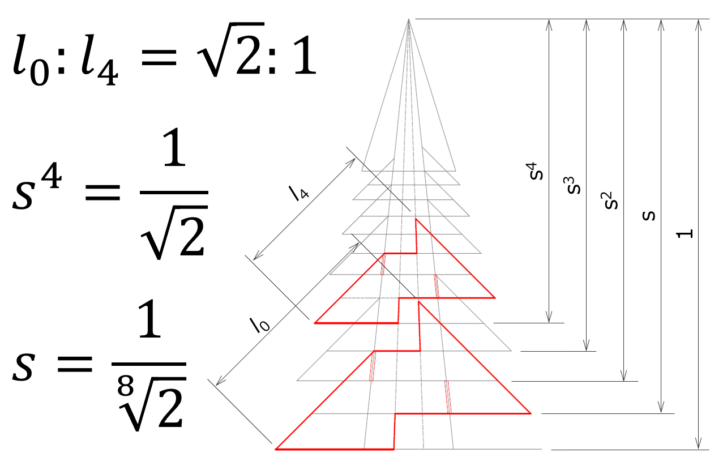
ある段と2つ上の段のサイズ(長さ)の比率が\(\sqrt{2}:1\)になるように縮小率sを決めます。こうすると、例えば一番下と2段目のパーツの図面をA3サイズで綺麗に作っておけば、あとはそれをA4、A5サイズに縮小コピーするだけで上の段の図面が出来上がるので楽ちんです。本当は1つ上の段との比率を\(\sqrt{2}:1\)にできれば良かったんですが、それだとツリーの枝の数が少なすぎて面白くないので、2段おきにしました。とにかく、縮小率sは作成の労力を小さくしようとすると自然と決まるのです。
枝の角度が45°になるようにtを決める
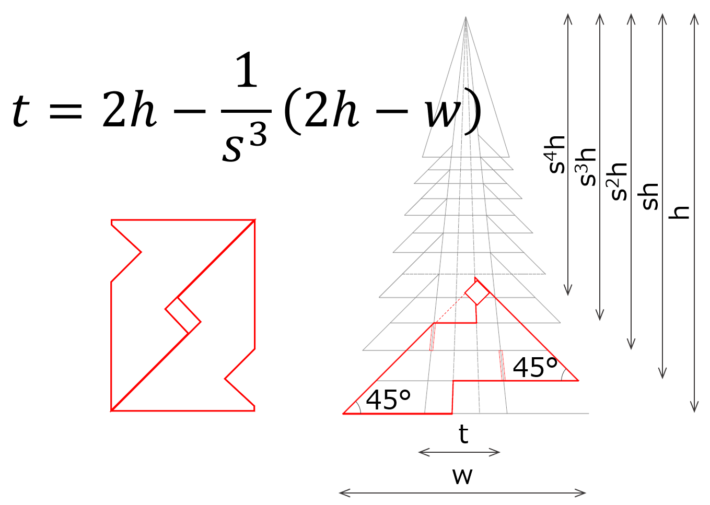
枝の角度を45°にすると、上の図のようにパーツを並べたときちょうど長方形になります。これの何がいいかって、ダンボールからパーツを取るとき無駄なく取れるのです。工作はそこらへんに転がっている廃材を利用してやるのが正しいお作法であり材料が潤沢にある訳ではありませんので、無駄なく材料が使えるというのは重要です。という訳でダンボールを有効利用したいと思うとtは必然的に上記の式となるのです。
素晴らしく没個性的なのに似たものがない?
これまでくどくどと説明したように、このダンボールクリスマスツリーは「できるだけ大きいクリスマスツリーを、限られたダンボール資材で、簡単かつ確実に作る」ための合理的な選択と計算によってほぼ全てがデザインされており、そこに個人のセンスや感覚やその日の気分が入り込む余地は全くといっていいほどありません。その意味でとても洗練された、素晴らしい没個性的工作作品だと自負しています。えっへん。
ここで、このダンボールクリスマスツリーが本当に「合理的な選択と計算」でできるなら、誰か他の人が同じように考えて似たものを作っていてもよさそうに思えます。しかし「ダンボール クリスマスツリー」などでググってみても似たようなものは出てきません。むしろ他の作例よりも個性的でオリジナリティがあるようにすら見えます。何故か?答えは簡単、 「できるだけ大きいクリスマスツリーを、限られたダンボール資材で、簡単かつ確実に作るにはどうしたらよいか?」 なんてどうでもいいことを大真面目に考える人なんて1人くらいしかいないからです(フェルミ推定するまでもないでしょう)。
「問いかけ」が大事という分不相応に壮大なシメ
ダンボールクリスマスツリーにちょっとだけ個性やオリジナリティを感じるのは 「できるだけ大きいクリスマスツリーを、限られたダンボール資材で、簡単かつ確実に作るにはどうしたらよいか?」 というちょっとだけ珍しい問いかけをしたからです。創作は、問いかけから答えに辿りつくまでの道のりです。正しい答えが何かってことは問いかけで決まるのであり、その道のりが前人未踏の荒野なのか綺麗に舗装された道かは本質的には問題ではありません。ただ珍しい答えは誰も踏み込んだことのない場所にあることが多いだけで。
そう考えると、冒頭で引用した言葉の意味もわかってきます。絵描きの女の子のショックは先人と同じものを作ったことではなく、自分の中に問いかけが無かったことなのでしょう。このままではどこにも行けないという怖さ、問いかけがあれば動けるのです(行った先に何があるかはわかりませんが)。
他にも、小説などで問いもなくただ先人の答えをなぞるだけなのが模倣、陳腐な質問から生まれたものがマンネリ、壮大な問いをするも途中で道に迷い座礁するのが若気の至り。そういうことなのですね。
昔読んだ著名なフィナンシャルプランナーの書いた金融リテラシーの本は、論旨明快、理路整然とした説明で初心者の私には大変役に立ったのですが、クソが付くほど退屈で面白くなくて二度と読む気になれませんでした。大して面白くもない質問から出発して高速道路を通ってイッキに目的地に着くことほど退屈なものはないね。



ディスカッション
コメント一覧
まだ、コメントがありません