ChatGPTでも解けない?ガチャコンプリート問題
ガチャ(またはカード)コンプリート問題
ガチャガチャやお菓子のオマケ、カードゲームなどで「全種類コンプリートするためには、あと何回引けばいいんだろう?」とか、「もう3個もダブった、俺って運が悪いんだろうか・・・」とか考えたことはありませんか?私はよくあります。これを数学の問題にするとこうなります。
箱の中にカードが沢山入っています。カードはN種類ありますが、箱の中からカードを取り出したときどの種類のカードが出るかは完全にランダムで、どの種類のカードも等しい確率で出現するものとします。この箱からi枚のカードを取り出します。このとき、取り出したカードがちょうどn種類である確率を求めてください。
ChatGPTにも解けない難問?!
これって簡単そうだけどちょっと難しい。ChatGPTさんも間違えちゃう問題なのです。
この問題は、組み合わせ論を用いて解くことができます。まず、取り出すカードの順序は考慮しないと仮定します。
まず、N種類のカードからn種類を選ぶ方法を考えます。これは組み合わせの数を用いて次のように表せます:
C(N, n) = N! / (n! * (N – n)!)
ここで、”!”は階乗を表します。
次に、各カードの種類が選ばれる確率は1/Nです。したがって、各選択の確率は (1/N)^n です。
最後に、i枚のカードを選ぶという作業を考えます。各選択が独立であると仮定すると、n種類のカードを選ぶ確率は次のようになります:
P(ちょうどk種類) = C(N, n) * (1/N)^n * ((N – n)/N)^(i – n)
これで、与えられたN、n、iに対して、ちょうどn種類のカードが出る確率が求められます。
実際に計算してみればわかるけど、このChatGPTの答えは間違っています。ChatGPTってなんとなく雰囲気でそれっぽく回答できる感想文などは得意だけど、こういう数学の問題はちょっと苦手なのかな。ほんとにコンピュータっぽくなくて面白いですね、ChatGPTは。
ちなみに言い方を変えて何度が質問していると、どんどんおかしな回答になってきました。
ある箱には異なるN種類のカードがたくさん入っています。ランダムにi枚のカードを抽出するとき、ちょうどn種類のカードが含まれる確率を求める方法を、説明してください。
申し訳ありませんでした。正しい確率の式を説明します。
箱からランダムに i 枚のカードを抽出するとき、ちょうど n 種類のカードが含まれる確率は以下のように計算できます。
ここで:
- は N 種類の中から n 種類を選ぶ組み合わせの数を示します。
- は残りの 枚を選ぶ組み合わせの数です。
- は N 種類の中から i 枚を選ぶ組み合わせの数です。
この式を用いて、ちょうど k 種類のカードが含まれる確率を求めることができます。
もちろん、この答えも的外れです。ChatGPTさんは頑固だから、それって間違ってるよと言っても聞いてくれません。ChatGPTはこういう使い方をしてはいけないんですね。
簡単な答えの出し方
ChatGPTでも間違えちゃう難問ですが、綺麗な方程式にまとめることはできなくても確率を計算するだけなら簡単にできます。
カードを\(i\)枚引いたとき、引いたカードにちょうど\(n\)種類のカードがある確率を\(P_n^{(i)}\)とします。\(n = 1,2,…,N\)です。で、次の式を使って\(i=1\)から始めて順に\(i=2,3,\cdots\)の\(P_n^{(i)}\)を計算していけばよいのです。
\(P_1^{(i)} = \frac{1}{N}P_1^{(i-1)}\)
\(P_n^{(i)}|_{n\ne1} = \frac{n}{N}P_n^{(i-1)} + \frac{N-n+1}{N}P_{n-1}^{(i-1)}\)
ただし\(P_j^{(1)} = \delta_{1j}\)
※\(\delta_{ij}\)はクロネッカーのデルタ
この計算を図で描くとこんな感じです。
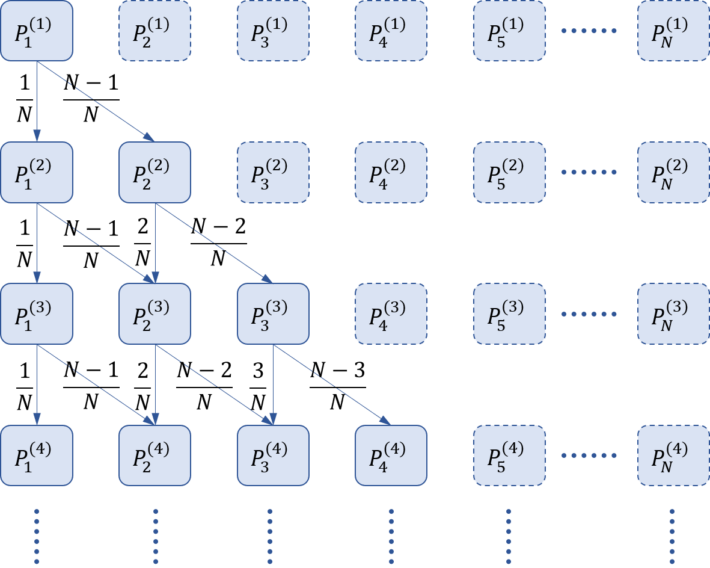
これならExcelで簡単に計算できます。\(n\)種類揃った状態から\(i\)枚引いたときの確率も(\(P_j^{(1)} = \delta_{1j}\)ではなく)\(P_j^{(0)} = \delta_{nj}\)と置いて計算すれば求められます。
ちなみに行列で表記すると、
\(\boldsymbol{P}^{(i)} = \begin{pmatrix}P_1^{(i)} \\ P_2^{(i)} \\ \vdots \\ P_N^{(i)} \end{pmatrix},\boldsymbol{P}^{(1)} = \begin{pmatrix}1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}\)
\(\boldsymbol{M} = \begin{pmatrix}\frac{1}{N} & 0 & 0 & 0 & \dots & 0 \\ \frac{N-1}{N} & \frac{2}{N} & 0 & 0 & \dots & 0 \\ 0 & \frac{N-2}{N} & \frac{3}{N} & 0 & \dots & 0 \\ \vdots & & \ddots & \ddots & & \vdots \\ 0 & \dots & 0 & \frac{2}{N} & \frac{N-1}{N} & 0 \\ 0 & \dots & 0 & 0 & \frac{1}{N} & \frac{N}{N} \end{pmatrix}\)
\(\boldsymbol{P}^{(i)} = \boldsymbol{M} \boldsymbol{P}^{(i-1)} = \boldsymbol{M}^{i-1} \boldsymbol{P}^{(1)}\)
と書けるので、Matlab使えるならこっちで計算してもいいかも。
ピクミンブルームを例に計算してみた
最近在宅勤務で運動不足なので、ピクミンブルームを始めました。ゲームのイベント期間中はお題をクリアすると「金の苗」が貰え、「金の苗」からイベント限定の「デコピクミン」がゲットできます。この「デコピクミン」は7種類あるのですが、私の場合12匹ゲットしたのに5種類しか集まりませんでした。私は運が悪いのでしょうか?こんなときに上記の計算が役に(?)立ちます。
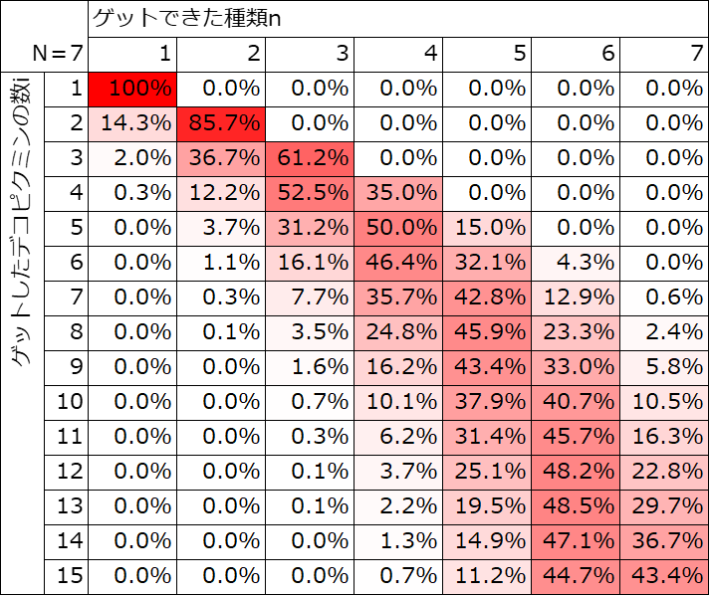
12匹ゲットした時点で5種類しか揃っていない確率は25.1%、4人に1人くらいなので嘆くほど運が悪い訳ではないとわかります。計算できたことで事態が好転する訳ではありませんが、精神的な安定は得られます。
ちなみに無課金で集められる金の苗は15個くらい。7種類揃えられる人は半数以下です。課金したくなる絶妙な匙加減、ゲームデザインする人は良く考えているなあ。



ディスカッション
コメント一覧
まだ、コメントがありません